Teza 1
Exercitiul 1. Enumerati elementele multimii \( A = \{ x | x \in \mathbb N \ \mbox{și} \ x \in \mathcal D_{14} \} \)
Exercitiul 2. Scrieti divizorii numarului 18.
Exercitiul 3. Din 30 kg de portocale se obtin 18 l de suc. Aflati cati litri de suc se obtin din 20 kg de portocale.
Exercitiul 4. Verificati proprietatea \( a \cdot b =(a,b)\cdot[a,b] \), pentru a = 24 si b = 36, unde \( (a,b) \) inseamna c.m.m.d.c al numerelor a si b, iar \([a,b]\) inseamna c.m.m.m.c al numerelor a si b.
Exercitiul 5. Se considera doua dreapte AB si CD concurente in punctul O. Daca \( \sphericalangle AOC = 70° \), calculati \( \sphericalangle BOD \)
Exercitiul 6. Masura arcului \( \overset{ \huge\frown}{AB} \) reprezinta 40% din masura cercului \( (O,r) \). Determinati masura unghiului la centru \( AOB \)
Exercitiul 7. Determinati x astfel incat dreptele a si b din figura urmatoare sa fie paralele.
Exercitiul 8. Cel mai mare divizor comun a doua numere este 15. Aflati numerele, stiind ca produsul lor este 3150.
Exercitiul 9. Raportul masurilor a doua dintre unghiurile formate de doua drepte concurente este egal cu \( \displaystyle \frac{2}{3} \). Aflati masurile unghiurilor.
Exercitiul 10. Se dau multimile \( A = \{ a,b,c \} \) si \( B = \{ b,d \} \). Calculati \( A \cup B \), \( A \cap B \) si \( A \setminus B \).
Exercitiul 11. Bisectoarele unghiurilor adiacente \( \sphericalangle AOB \) si \( \sphericalangle BOC \) formeaza un unghi cu masura de 60°. Stiind ca raportul masurilor celor doua unghiuri este \( \displaystyle \frac{2}{3} \), calculati :
- masura unghiului \( \sphericalangle AOC\);
- masura unghiului format de bisectoarea unghiului \( \sphericalangle AOB \) si semidreapta opusa semidreptei OB;
- masura unghiului format de bisectoarea unghiului \( \sphericalangle BOC \) si semidreapta opusa semidreptei OA.
Exercitiul 1
\( \begin{eqnarray} D_{14} = \{1,2,7,14\} \\ A = \{ 1,2,7,14 \} \end{eqnarray} \)
Exercitiul 2
\( D_{18} = \{1,2,3,6,9,18 \} \)
Exercitiul 3
30 kg portocale ........................... 18 litri suc
20 kg portocale ........................... x litri suc
\[ x = \frac{\cancel{20}\cancel{kg} \cdot \cancelto{6}{18}l}{\cancel{30}\cancel{kg}}= 12 \ \text{litri suc} \]
Exercitiul 4
\begin{align}
a \cdot b & = & (a\cdot b)\cdot[a,b] \\
\begin{array}{l} a = 24 \\ b = 36 \end{array} & \Longrightarrow & \underline{ \begin{cases} a = 2^3 \cdot 3 \\ b = 2^2 \cdot 3^2 \end{cases}} \\
&& (a,b) = 2^3\cdot3 = 12 \\
&& [a,b] = 2^3\cdot3^2 = 72 \\
24 \cdot 36 & = & 12 \cdot 72 \\
864 & = & 864 \ \ \text{(A)}
\end{align}
Exercitiul 5
| \begin{eqnarray} AB \cap CD = \{ 0 \} \\ \underline{\overset{ \huge\frown}{AB} =70°} \\ \overset{ \huge\frown}{BOD} = ? \end{eqnarray} |
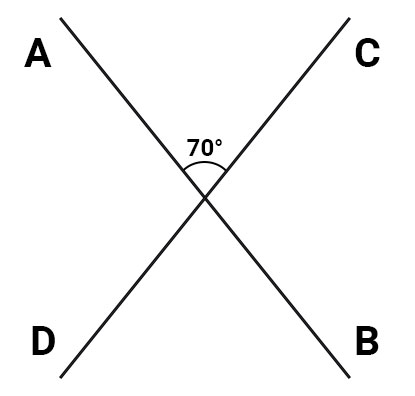 |
\( \left. \begin{aligned} OA \ & \text{si} \ OB \\ OC \ & \text{si} \ OD \end{aligned} \right\vert \ \text{perechi de semidrepte opuse} \ \Rightarrow \overset{\huge\frown}{AOC} \ \text{si} \ \overset{ \huge\frown}{AOB} \ \text{sunt} \) \( \sphericalangle \ \text{opuse la varf} \ \Rightarrow \overset{ \huge\frown}{BOD} \equiv \overset{ \huge\frown}{AOC} = 70° \)
Exercitiul 6
\(\underline{\overset{ \huge\frown}{AB} = 40° \cdot m[C(o,r)]} \)
\(\overset{\huge\frown}{AOB} = ? \)
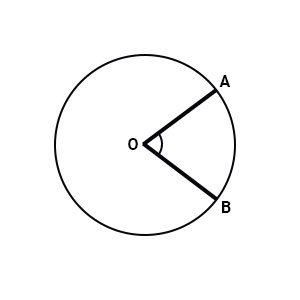 |
\begin{align}\overset{\huge\frown}{AOB} &= \ \text{unghi la centru} \\ m(\overset{ \huge\frown}{AOB}) &= m(\overset{ \huge\frown}{AB})\end{align} |
\[ \overset{ \huge\frown}{AB} = \frac{4\cancel{0}}{1\cancel{0}\cancel{0}} \cdot 36\cancel{0}° = 144° \]
Exercitiul 7
\( x = ? \ \text{a.i} \ a \parallel b \)
\( \text{Suplementul unghiului de} \ 135° = 180° - 135° = 45° \Rightarrow \) \( x° = 45° \ \text{(unghiuri corespondente)} \ \Rightarrow c \ \text{secantă} \ \Rightarrow a \parallel b \)
Exercitiul 8
\( (a,b) = 15 \)
\( \underline{ a\cdot b = 3150} \)
\( a,b = ? \)
\begin{align} \text{din} \ (a,b) = 15 & \Rightarrow & \ a =15 \cdot p \\ & & \ b = 15 \cdot K \\ & & \ (p,K) = 1 \\ & & \ p \in \mathbb{N}, K \in \mathbb{N} \\ a \cdot b = 15 \cdot p \cdot 15 \cdot K &=& 3150 \\ 225\cdot p \cdot K &=& 3150 \\ p\cdot K &=& 3150 : 225 \\ \left. \begin{array}{l} p\cdot K = 14 \\ \text{dar} \ (p,K) = 1 \end{array} \right\} \end{align}